
Veri Bilimine Yeni Başlayan Her Kişinin Bilmesi Gereken 15 Temel İstatistik Kavramı
Kalbinde veri bilimi Yüzyıllardır var olan ancak günümüzün dijital çağında temel olarak önemini koruyan istatistikler yatıyor. Neden? Çünkü temel istatistik kavramları temel istatistik kavramlarıdır. veri analizi, Her gün üretilen büyük miktarda veriyi anlamlandırmamızı sağlıyor. İstatistiklerin doğru soruları sormamıza ve verilerin anlatmaya çalıştığı hikayeleri anlamamıza yardımcı olduğu verilerle konuşmak gibidir.
İstatistikler, gelecekteki eğilimleri tahmin etmekten verilere dayalı kararlar almaya, hipotezleri test etmeye ve performansı ölçmeye kadar, veriye dayalı kararların ardındaki öngörüleri güçlendiren bir araçtır. Ham veriler ile eyleme dönüştürülebilir öngörüler arasındaki köprüdür ve onu veri biliminin vazgeçilmez bir parçası haline getirir. Bu yazıda, veri bilimine yeni başlayan her kişinin bilmesi gereken en önemli 15 temel istatistik kavramını derledim!
1. İstatistiksel Örnekleme ve Veri Toplama Bazı temel istatistik kavramlarını öğreneceğiz, ancak veri okyanusunun derinliklerine dalmadan önce verilerimizin nereden geldiğini ve bunları nasıl topladığımızı anlamak çok önemlidir. Popülasyonların, örneklerin ve çeşitli örnekleme tekniklerinin devreye girdiği yer burasıdır. Bir şehirdeki insanların ortalama boyunu bilmek istediğimizi düşünün. Herkesi ölçmek pratiktir, bu nedenle daha büyük nüfusu temsil eden daha küçük bir grubu (örneklem) alırız. İşin püf noktası bu örneği nasıl seçtiğimizde yatıyor. Rastgele, katmanlı veya küme örneklemesi gibi teknikler, örneğimizin iyi temsil edilmesini sağlayarak önyargıyı en aza indirir ve bulgularımızı daha güvenilir hale getirir. Popülasyonları ve örnekleri anlayarak, içgörülerimizi örneklemden tüm popülasyona güvenle genişletebilir ve herkesi araştırmaya gerek kalmadan bilinçli kararlar verebiliriz. 2. Veri Türleri ve Ölçüm Ölçekleri Veriler çeşitli şekillerde gelir ve uğraştığınız veri türünü bilmek, doğru istatistiksel araçları ve teknikleri seçmek için çok önemlidir. Nicel ve Nitel Veriler Nicel Veriler: Bu tür veriler tamamen sayılarla ilgilidir. Ölçülebilir ve matematiksel hesaplamalar için kullanılabilir. Nicel veriler bize bir web sitesini ziyaret eden kullanıcı sayısı veya bir şehrin sıcaklığı gibi “ne kadar” veya “kaç tane” olduğunu söyler. Sayısal değerler aracılığıyla net bir resim sağlayan basit ve objektiftir. Nitel Veriler: Tersine, nitel veriler özellikler ve açıklamalarla ilgilenir. Bu “hangi tür” veya “hangi kategori” ile ilgilidir. Bunu, bir arabanın rengi veya bir kitabın türü gibi nitelikleri veya nitelikleri tanımlayan veriler olarak düşünün. Bu veriler subjektiftir ve ölçümlerden ziyade gözlemlere dayanmaktadır. Dört Ölçüm Ölçeği Nominal ölçek: Bu, verileri belirli bir sıra olmadan kategorize etmek için kullanılan en basit ölçüm şeklidir. Örnekler arasında mutfak türleri, kan grupları veya milliyet yer alır. Herhangi bir niceliksel değeri olmayan etiketlemeyle ilgilidir. Sıra Ölçeği: Veriler burada sıralanabilir veya sıralanabilir ancak değerler arasındaki aralıklar tanımlanmamıştır. Memnun, nötr ve memnun değil gibi seçeneklerin bulunduğu bir memnuniyet anketi düşünün. Bize sıralamayı söyler ancak sıralamalar arasındaki mesafeyi söylemez. Aralık Ölçeği: Aralık, sipariş verilerini ölçeklendirir ve girişler arasındaki farkı ölçer. Ancak gerçekte sıfır noktası yoktur. Bunun iyi bir örneği Santigrat cinsinden sıcaklıktır; 10°C ile 20°C arasındaki fark, 20°C ile 30°C arasındaki farkla aynıdır ancak 0°C, sıcaklığın olmadığı anlamına gelmez. Oran ölçeği: En bilgilendirici ölçek, aralık ölçeğinin tüm özelliklerine artı anlamlı bir sıfır noktasına sahiptir ve büyüklüklerin doğru bir şekilde karşılaştırılmasına olanak tanır. Örnekler arasında ağırlık, boy ve gelir yer alır. Burada bir şeyin diğerinin iki katı olduğunu söyleyebiliriz. 3. Tanımlayıcı istatistikler Hayal etmek tanımlayıcı istatistikler verilerinizle ilk randevunuz olarak. Bu, önünüzde olanı tanımlayan temelleri ve geniş çizgileri tanımakla ilgilidir. Tanımlayıcı istatistiklerin iki ana türü vardır: merkezi eğilim ve değişkenlik ölçümleri. Merkezi Eğilim Ölçüleri: Bunlar verinin ağırlık merkezi gibidir. Bize veri setimizin tipik veya temsilcisi olan tek bir değer verirler. Anlamına gelmek: Ortalama, tüm değerlerin toplanması ve değer sayısına bölünmesiyle hesaplanır. Bu, bir restoranın tüm incelemelere dayalı genel puanı gibidir. Ortalamanın matematiksel formülü aşağıda verilmiştir:

Medyan: Veriler küçükten büyüğe sıralandığında ortadaki değer. Gözlem sayısı çift ise ortadaki iki sayının ortalamasıdır. Köprünün orta noktasını bulmak için kullanılır.
Eğer n çift ise medyan iki merkezi sayının ortalamasıdır.

Modu: It is Bir veri setinde en sık tekrarlanan değer. Bunu bir restorandaki en popüler yemek olarak düşünün.
Değişkenlik Ölçüleri: Merkezi eğilim ölçüleri bizi merkeze getirirken, değişkenlik ölçüleri bize yayılma veya dağılım hakkında bilgi verir.
Menzil: En yüksek ve en düşük değerler arasındaki fark. Yayılım hakkında temel bir fikir verir.

Varyans: Kümedeki her sayının ortalamadan ve dolayısıyla kümedeki diğer tüm sayılardan ne kadar uzakta olduğunu ölçer. Örnek olarak şu şekilde hesaplanır:

Standart sapma: Varyansın karekökü ortalamaya olan ortalama mesafenin bir ölçüsünü sağlar. Bu, bir fırıncının kek boyutlarının tutarlılığını değerlendirmek gibidir. Şu şekilde temsil edilir:

Bir sonraki temel istatistik kavramına geçmeden önce, burada bir Yeni Başlayanlar İçin İstatistiksel Analiz Kılavuzu sizin için!
4. Veri GörselleştirmeVeri goruntuleme verilerle hikaye anlatma sanatı ve bilimidir. Analizimizin karmaşık sonuçlarını somut ve anlaşılır bir şeye dönüştürür. Hedefin henüz resmi sonuçlara varmadan verilerden kalıpları, korelasyonları ve içgörüleri ortaya çıkarmak olduğu keşfedici veri analizi için bu çok önemlidir.
- Grafikler ve grafikler: Temel bilgilerden başlayarak çubuk grafikler, çizgi grafikler ve pasta grafikler verilere ilişkin temel bilgiler sağlar. Bunlar, herhangi bir veri hikayesi anlatıcı için gerekli olan veri görselleştirmenin ABC'leridir.
Aşağıda bir çubuk grafiği (solda) ve bir çizgi grafiği (sağda) örneğimiz var.

- Gelişmiş Görselleştirmeler: Daha derine indikçe ısı haritaları, dağılım grafikleri ve histogramlar daha ayrıntılı analizlere olanak tanır. Bu araçlar eğilimleri, dağılımları ve aykırı değerleri belirlemeye yardımcı olur.
Aşağıda bir dağılım grafiği ve histogram örneği verilmiştir

Görselleştirmeler, ham veriler ile insan bilişi arasında köprü kurarak karmaşık veri kümelerini hızlı bir şekilde yorumlamamıza ve anlamlandırmamıza olanak tanır.
5. Olasılık TemelleriOlasılık istatistik dilinin grameridir. Olayların gerçekleşme şansı veya olasılığı ile ilgilidir. Olasılıktaki kavramları anlamak, istatistiksel sonuçları yorumlamak ve tahminlerde bulunmak için gereklidir.
- Bağımsız ve Bağımlı Olaylar:
- Bağımsız Etkinlikler: Bir olayın sonucu diğerinin sonucunu etkilemez. Yazı tura atmak gibi, bir atışta tura gelmesi bir sonraki atışın şansını değiştirmez.
- Bağımlı Olaylar: Bir olayın sonucu diğerinin sonucunu etkiler. Örneğin, bir desteden bir kart çekerseniz ve onu değiştirmezseniz, başka bir özel kart çekme şansınız değişir.
Olasılık, veriler hakkında çıkarımlar yapmak için temel sağlar ve istatistiksel anlamlılığın ve hipotez testlerinin anlaşılması açısından kritik öneme sahiptir.
6. Ortak Olasılık DağılımlarıOlasılık dağılımları istatistik ekosistemindeki farklı türler gibidir ve her biri kendi uygulama alanına uyarlanmıştır.
- Normal dağılım: Şekli nedeniyle sıklıkla çan eğrisi olarak adlandırılan bu dağılım, ortalaması ve standart sapması ile karakterize edilir. Birçok istatistiksel testte bu yaygın bir varsayımdır çünkü birçok değişken gerçek dünyada doğal olarak bu şekilde dağıtılır.

Ampirik kural veya 68-95-99.7 kuralı olarak bilinen bir dizi kural, verilerin ortalama etrafında nasıl yayıldığını açıklayan normal dağılımın özelliklerini özetler.
68-95-99.7 Kuralı (Deneysel Kural)Bu kural tamamen normal bir dağılım için geçerlidir ve aşağıdakileri özetlemektedir:
- %68 Verilerin yüzdesi ortalamanın (μ) bir standart sapması (σ) dahilindedir.
- %95 Verilerin yüzdesi ortalamanın iki standart sapması dahilindedir.
- Yaklaşık olarak %99.7 Verilerin yüzdesi ortalamanın üç standart sapması dahilindedir.
Binom dağılımı: Bu dağılım, iki sonucun (başarı veya başarısızlık gibi) birkaç kez tekrarlandığı durumlar için geçerlidir. Yazı tura atma veya doğru/yanlış testi yapma gibi olayların modellenmesine yardımcı olur.
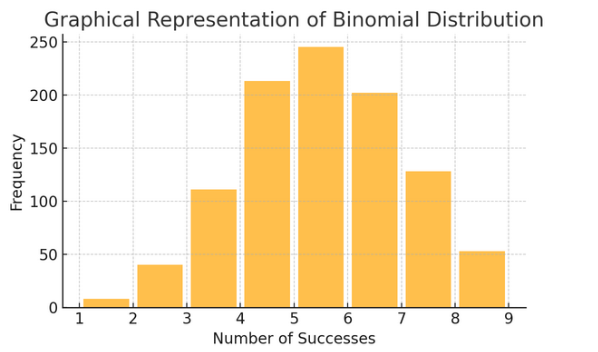
Poisson Dağılımı belirli bir aralık veya alanda bir şeyin kaç kez gerçekleştiğini sayar. Aldığınız günlük e-postalar gibi olayların bağımsız ve sürekli olarak gerçekleştiği durumlar için idealdir.
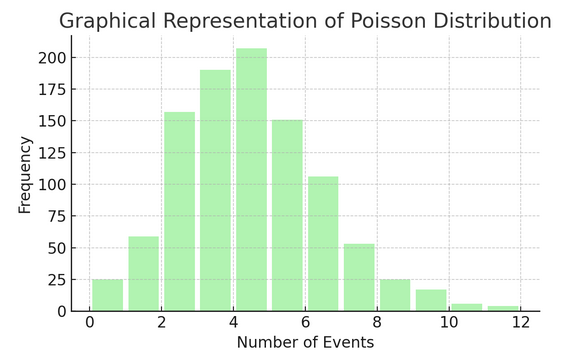
Her dağıtımın kendine ait formülleri ve özellikleri vardır ve doğru olanı seçmek, verilerinizin doğasına ve ne bulmaya çalıştığınıza bağlıdır. Bu dağılımları anlamak, istatistikçilerin ve veri bilimcilerinin gerçek dünyadaki olayları modellemelerine ve gelecekteki olayları doğru bir şekilde tahmin etmelerine olanak tanır.
7. Hipotez testi
Düşünmek hipotez testi istatistikte dedektiflik çalışması olarak. Verilerimiz hakkındaki belirli bir teorinin doğru olup olmadığını test etmek için kullanılan bir yöntemdir. Bu süreç iki karşıt hipotezle başlar:
- Sıfır Hipotezi (H0): Bu, bir etki veya fark olduğunu öne süren varsayılan varsayımdır. Burada "yeni değil" diyor.
- Al “alternatif Hipotez (H1 veya Ha): Bu, bir etki ya da farklılık önererek statükoya meydan okuyor. “İlginç bir şeyler oluyor” iddiasında bulunuyor.
Örnek: Yeni bir diyet programının herhangi bir diyet uygulamamaya kıyasla kilo kaybına yol açıp açmadığını test etmek.
- Sıfır Hipotezi (H0): Yeni diyet programı kilo kaybına yol açmıyor (yeni diyet programını uygulayanlarla uygulamayanlar arasında kilo kaybı açısından bir fark yok).
- Alternatif Hipotez (H1): Yeni diyet programı kilo kaybına neden oluyor (uygulayanlarla uygulamayanlar arasında kilo kaybı açısından fark var).
Hipotez testi, kanıtlara (verilerimize) dayanarak bu ikisi arasında seçim yapmayı içerir.
Tip I ve II Hata ve Önem Düzeyleri:- Tip I Hatası: Bu, sıfır hipotezini hatalı bir şekilde reddettiğimizde olur. Masum bir insanı mahkum ediyor.
- Tip II Hata: Bu, yanlış bir sıfır hipotezini reddetmeyi başaramadığımızda ortaya çıkar. Suçlu bir kişinin serbest kalmasına izin verir.
- Önem Düzeyi (α): Bu Sıfır hipotezini reddetmek için ne kadar kanıtın yeterli olduğuna karar verme eşiği. Genellikle %5 (0.05) olarak ayarlanır ve bu da %5 Tip I hata riskini belirtir.
8. Güven Aralıkları
Güvenilirlik aralığı bize geçerli nüfus parametresinin (ortalama veya oran gibi) belirli bir güven düzeyiyle (genellikle %95) düşmesini beklediğimiz bir değerler aralığı verin. Bu, bir spor takımının final skorunu hata payı ile tahmin etmeye benzer; "Gerçek puanın bu aralıkta olacağından %95 eminiz" diyoruz.
Güven aralıklarını oluşturmak ve yorumlamak, tahminlerimizin kesinliğini anlamamıza yardımcı olur. Aralık ne kadar geniş olursa tahminimiz o kadar kesin olmaz ve bunun tersi de geçerlidir.
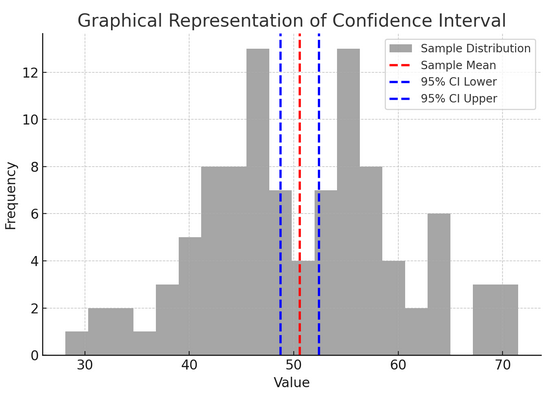
Yukarıdaki şekil istatistiklerdeki güven aralığı (CI) kavramını bir örneklem dağılımı ve bunun örnek ortalaması etrafındaki %95 güven aralığını kullanarak göstermektedir.
Şekildeki kritik bileşenlerin dökümü aşağıda verilmiştir:
- Örnek Dağılımı (Gri Histogram): Bu, ortalaması 100 ve standart sapması 50 olan normal bir dağılımdan rastgele oluşturulan 10 veri noktasının dağılımını temsil eder. Histogram, veri noktalarının ortalama etrafında nasıl yayıldığını görsel olarak gösterir.
- Örnek Ortalama (Kırmızı Kesikli Çizgi): Bu satır örnek verilerin ortalama (ortalama) değerini gösterir. Güven aralığını oluşturduğumuz nokta tahmini olarak hizmet eder. Bu durumda tüm örnek değerlerin ortalamasını temsil eder.
- %95 Güven Aralığı (Mavi Kesikli Çizgiler): Bu iki çizgi, örnek ortalaması etrafındaki %95 güven aralığının alt ve üst sınırlarını işaretler. Aralık, ortalamanın standart hatası (SEM) ve istenen güven düzeyine karşılık gelen bir Z puanı (%1.96 güven için 95) kullanılarak hesaplanır. Güven aralığı, popülasyon ortalamasının bu aralıkta olduğundan %95 emin olduğumuzu göstermektedir.
9. Korelasyon ve Nedensellik
Korelasyon ve nedensellik sıklıkla karıştırılır, ancak bunlar farklıdır:
- korelasyon: İki değişken arasındaki ilişkiyi veya ilişkiyi belirtir. Biri değiştiğinde diğeri de değişme eğilimindedir. Korelasyon, -1 ile 1 arasında değişen bir korelasyon katsayısıyla ölçülür. 1 veya -1'e yakın bir değer, güçlü bir ilişkiyi belirtirken, 0, herhangi bir bağ olmadığını belirtir.
- nedensellik: Bir değişkendeki değişikliğin doğrudan diğerinde değişikliğe neden olduğu anlamına gelir. Korelasyondan daha sağlam bir iddiadır ve sıkı testler gerektirir.
İki değişkenin ilişkili olması birinin diğerine neden olduğu anlamına gelmez. Bu, "korelasyonu" "nedensellik" ile karıştırmamanın klasik bir örneğidir.
10. Basit Doğrusal Regresyon
Basit doğrusal regresyon gözlemlenen verilere doğrusal bir denklem uydurarak iki değişken arasındaki ilişkiyi modellemenin bir yoludur. Değişkenlerden biri açıklayıcı değişken (bağımsız), diğeri ise bağımlı değişken olarak kabul edilir.
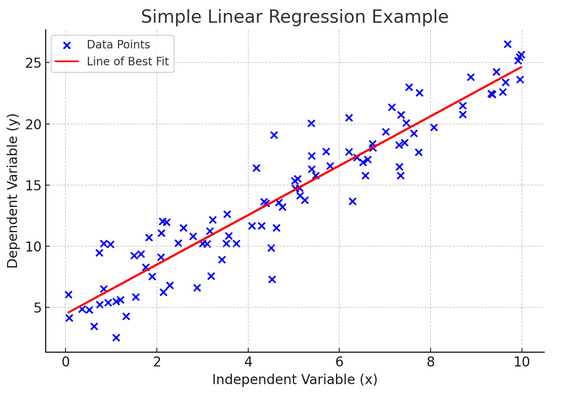
Basit doğrusal regresyon, bağımsız değişkendeki değişikliklerin bağımlı değişkeni nasıl etkilediğini anlamamıza yardımcı olur. Tahmin için güçlü bir araçtır ve diğer birçok karmaşık istatistiksel modelin temelini oluşturur. İki değişken arasındaki ilişkiyi analiz ederek, bunların nasıl etkileşime girecekleri konusunda bilinçli tahminler yapabiliriz.
Basit doğrusal regresyon, bağımsız değişken (açıklayıcı değişken) ile bağımlı değişken arasında doğrusal bir ilişki olduğunu varsayar. Bu iki değişken arasındaki ilişki doğrusal değilse, basit doğrusal regresyonun varsayımları ihlal edilebilir ve potansiyel olarak hatalı tahminlere veya yorumlara yol açabilir. Bu nedenle, basit doğrusal regresyon uygulanmadan önce verilerdeki doğrusal ilişkinin doğrulanması önemlidir.
11. Çoklu Doğrusal Regresyon
Çoklu doğrusal regresyonu, basit doğrusal regresyonun bir uzantısı olarak düşünün. Yine de, parlak zırhlı bir şövalyeyle (tahmin edici) sonucu tahmin etmeye çalışmak yerine, bütün bir takımınız var. Bu, bire bir basketbol maçından, her oyuncunun (tahmin edicinin) benzersiz beceriler getirdiği tam bir takım çalışmasına geçiş yapmak gibidir. Buradaki fikir, birkaç değişkenin birlikte tek bir sonucu nasıl etkilediğini görmektir.
Ancak daha büyük bir ekiple birlikte çoklu bağlantı olarak bilinen ilişkileri yönetme zorluğu da ortaya çıkar. Tahminciler birbirine çok yakın olduğunda ve benzer bilgileri paylaştığında ortaya çıkar. Sürekli olarak aynı şutu atmaya çalışan iki basketbolcuyu hayal edin; birbirlerinin yoluna çıkabilirler. Regresyon, her öngörücünün benzersiz katkısını görmeyi zorlaştırabilir ve potansiyel olarak hangi değişkenlerin önemli olduğuna dair anlayışımızı çarpıtabilir.
12. Lojistik Regresyon
Doğrusal regresyon sürekli sonuçları (sıcaklık veya fiyatlar gibi) tahmin ederken, lojistik regresyon Sonuç kesin olduğunda (evet/hayır, kazan/kaybet gibi) kullanılır. Çeşitli faktörlere dayanarak bir takımın kazanıp kazanmayacağını tahmin etmeye çalıştığınızı hayal edin; lojistik regresyon sizin stratejinizdir.
Doğrusal denklemi, çıktısı belirli bir kategoriye ait olma olasılığını temsil eden 0 ile 1 arasında olacak şekilde dönüştürür. Bu, sürekli puanları net bir "şu veya bu" görünümüne dönüştüren ve kategorik sonuçları tahmin etmemize olanak tanıyan sihirli bir merceğe sahip olmak gibidir.
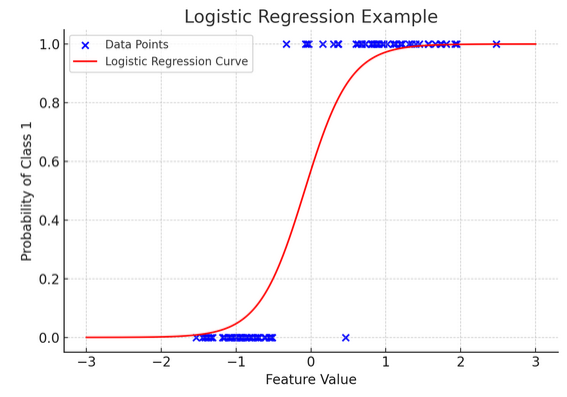
Grafiksel gösterim, sentetik ikili sınıflandırma veri kümesine uygulanan lojistik regresyonun bir örneğini göstermektedir. Mavi noktalar veri noktalarını temsil eder; bunların x ekseni boyunca konumları özellik değerini, y ekseni ise kategoriyi (0 veya 1) gösterir. Kırmızı eğri, lojistik regresyon modelinin, farklı özellik değerleri için sınıf 1'e (örneğin, “kazanma”) ait olma olasılığına ilişkin tahminini temsil eder. Gördüğünüz gibi eğri, sınıf 0 olasılığından sınıf 1 olasılığına sorunsuz bir şekilde geçiş yapıyor ve bu da modelin, temeldeki sürekli özelliğe dayalı olarak kategorik sonuçları tahmin etme yeteneğini gösteriyor.
Lojistik regresyon formülü şu şekilde verilir:

Bu formül, doğrusal denklemin çıktısını 0 ile 1 arasında bir olasılığa dönüştürmek için lojistik fonksiyonunu kullanır. Bu dönüşüm, çıktıları, bağımsız değişken xx'in değerine dayalı olarak belirli bir kategoriye ait olma olasılıkları olarak yorumlamamıza olanak tanır.
13. ANOVA ve Ki-Kare Testleri
ANOVA (Varyans Analizi) ve Ki-Kare testleri istatistik dünyasındaki dedektifler gibi farklı gizemleri çözmemize yardımcı oluyorlar. BENt en az birinin istatistiksel olarak farklı olup olmadığını görmek için birden fazla gruptaki ortalamaları karşılaştırmamıza olanak tanır. Bunu, herhangi bir partinin tadının önemli ölçüde farklı olup olmadığını belirlemek için birkaç kurabiye partisinden numuneleri tatmak olarak düşünün.
Kategorik veriler için ise Ki-Kare testi kullanılmaktadır. İki kategorik değişken arasında anlamlı bir ilişki olup olmadığını anlamamıza yardımcı olur. Mesela kişinin en sevdiği müzik türü ile yaş grubu arasında bir ilişki var mıdır? Ki-Kare testi bu tür soruların yanıtlanmasına yardımcı olur.
14. Merkezi Limit Teoremi ve Veri Bilimindeki Önemi
The Merkezi Limit Teoremi (CLT) neredeyse büyülü hissettiren temel bir istatistiksel prensiptir. Bu bize, bir popülasyondan yeterli sayıda örnek alıp bunların ortalamalarını hesaplarsanız, bu ortalamaların, popülasyonun orijinal dağılımından bağımsız olarak normal bir dağılım (çan eğrisi) oluşturacağını söyler. Bu inanılmaz derecede güçlü çünkü tam dağılımlarını bilmesek bile popülasyonlar hakkında çıkarımlar yapmamızı sağlıyor.
Veri biliminde CLT birçok tekniğin temelini oluşturarak, verilerimiz başlangıçta bu kriterleri karşılamasa bile normal şekilde dağıtılan veriler için tasarlanmış araçları kullanmamıza olanak tanır. Bu, istatistiksel yöntemler için evrensel bir adaptör bulmak, birçok güçlü aracı daha fazla durumda uygulanabilir hale getirmek gibidir.
15. Önyargı-Varyans Dengesi
In tahmine dayalı modelleme ve makine öğrenme, önyargı-varyans değiş tokuşu modellerimizin ters gitmesine neden olabilecek iki ana hata türü arasındaki gerilimi vurgulayan çok önemli bir kavramdır. Önyargı, altta yatan eğilimleri iyi yakalayamayan aşırı basit modellerden kaynaklanan hataları ifade eder. Eğimli bir yola düz bir çizgi sığdırmaya çalıştığınızı hayal edin; işareti kaçıracaksın. Tersine, çok karmaşık modellerden gelen Varyanslar, verilerdeki gürültüyü sanki gerçek bir modelmiş gibi yakalar; her kıvrımı takip etmek ve engebeli bir yolda ilerlemek ve bunun ileriye giden yol olduğunu düşünmek gibi.
İşin püf noktası, toplam hatayı en aza indirmek için bu ikisini dengelemek, modelinizin tam olarak doğru olduğu tatlı noktayı bulmaktır; doğru modelleri yakalayacak kadar karmaşık, ancak rastgele gürültüyü göz ardı edecek kadar basit. Bir gitarı akort etmeye benzer; çok sıkı ya da gevşekse kulağa doğru gelmiyor. Önyargı-varyans değişimi bu ikisi arasındaki mükemmel dengeyi bulmakla ilgilidir. Önyargı-varyans değiş tokuşu, istatistiksel modellerimizi, sonuçları doğru bir şekilde tahmin etmede ellerinden gelenin en iyisini yapacak şekilde ayarlamanın özüdür.
Sonuç
İstatistiksel örneklemeden önyargı-varyans değiş tokuşuna kadar, bu ilkeler yalnızca akademik kavramlar değil aynı zamanda anlayışlı veri analizi için temel araçlardır. Gelecek vaat eden veri bilimcilerini, büyük verileri eyleme geçirilebilir içgörülere dönüştürme becerileriyle donatıyorlar ve istatistiklerin dijital çağda veriye dayalı karar vermenin ve inovasyonun omurgası olduğunu vurguluyorlar.





